Android Draw Partial Circle on Canvas

Skip to master content

Three Ways to Describe an Arc

• Article
• 07/08/2021
• 16 minutes to read

Is this folio helpful?

Feedback will be sent to Microsoft: By pressing the submit button, your feedback will be used to improve Microsoft products and services. Privacy policy.

In this article

Download the sample

Acquire how to utilize SkiaSharp to define arcs in iii unlike ways

An arc is a bend on the circumference of an ellipse, such as the rounded parts of this infinity sign:

Despite the simplicity of that definition, there is no manner to define an arc-cartoon part that satisfies every need, and hence, no consensus amid graphics systems of the best way to draw an arc. For this reason, the SKPath course does non restrict itself to simply one approach.

SKPath defines an AddArc method, five different ArcTo methods, and two relative RArcTo methods. These methods fall into iii categories, representing three very different approaches to specifying an arc. Which one y'all use depends on the information available to define the arc, and how this arc fits in with the other graphics that you're drawing.

The Angle Arc

The angle arc approach to cartoon arcs requires that you specify a rectangle that premises an ellipse. The arc on the circumference of this ellipse is indicated by angles from the center of the ellipse that betoken the beginning of the arc and its length. Two unlike methods depict angle arcs. These are the AddArc method and the ArcTo method:

              public void AddArc (SKRect oval, Single startAngle, Single sweepAngle)  public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)                          

These methods are identical to the Android AddArc and [ArcTo]xref:Android.Graphics.Path.ArcTo*) methods. The iOS AddArc method is similar but is restricted to arcs on the circumference of a circle rather than generalized to an ellipse.

Both methods brainstorm with an SKRect value that defines both the location and size of an ellipse:

The arc is a part of the circumference of this ellipse.

The startAngle argument is a clockwise angle in degrees relative to a horizontal line drawn from the heart of the ellipse to the right. The sweepAngle argument is relative to the startAngle. Here are startAngle and sweepAngle values of 60 degrees and 100 degrees, respectively:

The arc begins at the commencement angle. Its length is governed by the sweep bending. The arc is shown here in cherry-red:

The bend added to the path with the AddArc or ArcTo method is simply that part of the ellipse's circumference:

The startAngle or sweepAngle arguments tin be negative: The arc is clockwise for positive values of sweepAngle and counter-clockwise for negative values.

Withal, AddArc does not ascertain a closed contour. If you call LineTo after AddArc, a line is drawn from the end of the arc to the point in the LineTo method, and the same is true of ArcTo.

AddArc automatically starts a new contour and is functionally equivalent to a call to ArcTo with a final argument of truthful:

              path.ArcTo (oval, startAngle, sweepAngle, true);                          

That last statement is called forceMoveTo, and it finer causes a MoveTo call at the beginning of the arc. That begins a new contour. That is non the example with a last statement of fake:

              path.ArcTo (oval, startAngle, sweepAngle, false);                          

This version of ArcTo draws a line from the current position to the showtime of the arc. This means that the arc can exist somewhere in the middle of a larger contour.

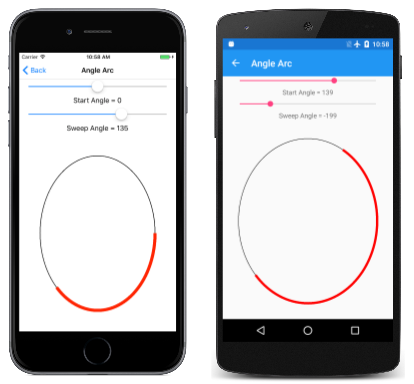
The Angle Arc page lets you use two sliders to specify the start and sweep angles. The XAML file instantiates two Slider elements and an SKCanvasView. The PaintCanvas handler in the AngleArcPage.xaml.cs file draws both the oval and the arc using two SKPaint objects defined equally fields:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas canvass = surface.Sail;      canvas.Clear();      SKRect rect = new SKRect(100, 100, info.Width - 100, info.Peak - 100);     float startAngle = (bladder)startAngleSlider.Value;     bladder sweepAngle = (float)sweepAngleSlider.Value;      sail.DrawOval(rect, outlinePaint);      using (SKPath path = new SKPath())     {         path.AddArc(rect, startAngle, sweepAngle);         canvas.DrawPath(path, arcPaint);     } }                          

As yous can meet, both the first angle and the sweep angle tin can take on negative values:

This approach to generating an arc is algorithmically the simplest, and information technology's easy to derive the parametric equations that depict the arc. Knowing the size and location of the ellipse, and the offset and sweep angles, the start and end points of the arc can be calculated using simple trigonometry:

x = oval.MidX + (oval.Width / two) * cos(bending)

y = oval.MidY + (oval.Height / 2) * sin(bending)

The angle value is either startAngle or startAngle + sweepAngle.

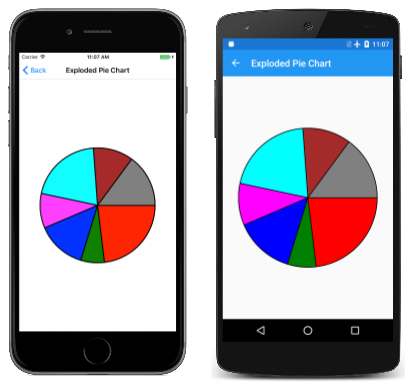
The use of two angles to ascertain an arc is all-time for cases where you know the angular length of the arc that you want to describe, for instance, to make a pie chart. The Exploded Pie Chart page demonstrates this. The ExplodedPieChartPage grade uses an internal class to ascertain some fabricated data and colors:

              course ChartData {     public ChartData(int value, SKColor colour)     {         Value = value;         Color = color;     }      public int Value { private set; get; }      public SKColor Colour { individual set; get; } }  ChartData[] chartData = {     new ChartData(45, SKColors.Red),     new ChartData(13, SKColors.Green),     new ChartData(27, SKColors.Blue),     new ChartData(19, SKColors.Magenta),     new ChartData(twoscore, SKColors.Cyan),     new ChartData(22, SKColors.Brown),     new ChartData(29, SKColors.Gray) };                          

The PaintSurface handler starting time loops through the items to calculate a totalValues number. From that, it can determine each item'southward size as the fraction of the total, and convert that to an bending:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas canvas = surface.Canvas;      canvas.Articulate();      int totalValues = 0;      foreach (ChartData item in chartData)     {         totalValues += item.Value;     }      SKPoint middle = new SKPoint(info.Width / two, info.Top / two);     bladder explodeOffset = fifty;     float radius = Math.Min(info.Width / ii, info.Meridian / ii) - 2 * explodeOffset;     SKRect rect = new SKRect(center.X - radius, middle.Y - radius,                              center.Ten + radius, center.Y + radius);      bladder startAngle = 0;      foreach (ChartData particular in chartData)     {         float sweepAngle = 360f * item.Value / totalValues;          using (SKPath path = new SKPath())         using (SKPaint fillPaint = new SKPaint())         using (SKPaint outlinePaint = new SKPaint())         {             path.MoveTo(center);             path.ArcTo(rect, startAngle, sweepAngle, false);             path.Close();              fillPaint.Way = SKPaintStyle.Fill;             fillPaint.Color = detail.Color;              outlinePaint.Fashion = SKPaintStyle.Stroke;             outlinePaint.StrokeWidth = v;             outlinePaint.Color = SKColors.Black;              // Summate "explode" transform             bladder bending = startAngle + 0.5f * sweepAngle;             float x = explodeOffset * (float)Math.Cos(Math.PI * bending / 180);             bladder y = explodeOffset * (bladder)Math.Sin(Math.PI * angle / 180);              canvas.Relieve();             sheet.Translate(x, y);              // Fill and stroke the path             canvas.DrawPath(path, fillPaint);             canvass.DrawPath(path, outlinePaint);             sail.Restore();         }          startAngle += sweepAngle;     } }                          

A new SKPath object is created for each pie piece. The path consists of a line from the eye, and then an ArcTo to draw the arc, and another line back to the center results from the Close call. This plan displays "exploded" pie slices by moving them all out from the center by l pixels. That task requires a vector in the direction of the midpoint of the sweep angle for each piece:

To come across what it looks similar without the "explosion," merely comment out the Translate call:

The Tangent Arc

The second blazon of arc supported past SKPath is the tangent arc, and so called because the arc is the circumference of a circumvolve that is tangent to two connected lines.

A tangent arc is added to a path with a call to the ArcTo method with two SKPoint parameters, or the ArcTo overload with separate Single parameters for the points:

              public void ArcTo (SKPoint point1, SKPoint point2, Single radius)  public void ArcTo (Single x1, Single y1, Single x2, Unmarried y2, Single radius)                          

This ArcTo method is like to the PostScript arct (folio 532) role and the iOS AddArcToPoint method.

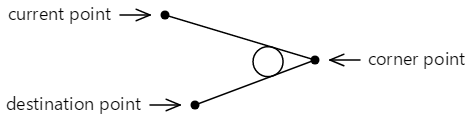
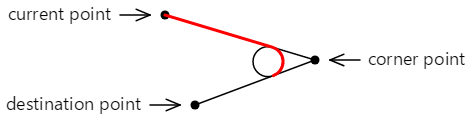
The ArcTo method involves three points:

• The current point of the contour, or the point (0, 0) if MoveTo has not been called
• The first signal statement to the ArcTo method, called the corner point
• The second point argument to ArcTo, called the destination point:

These iii points define two connected lines:

If the three points are colinear — that is, if they lie on the same direct line — no arc will be fatigued.

The ArcTo method also includes a radius parameter. This defines the radius of a circle:

The tangent arc is not generalized for an ellipse.

If the ii lines encounter at any angle, that circumvolve can be inserted between those lines and so that it is tangent to both lines:

The curve that is added to the profile does not touch on either of the points specified in the ArcTo method. It consists of a direct line from the current bespeak to the start tangent bespeak, and an arc that ends at the second tangent signal, shown here in cherry:

Here's the terminal straight line and arc that is added to the contour:

The contour can exist continued from the second tangent point.

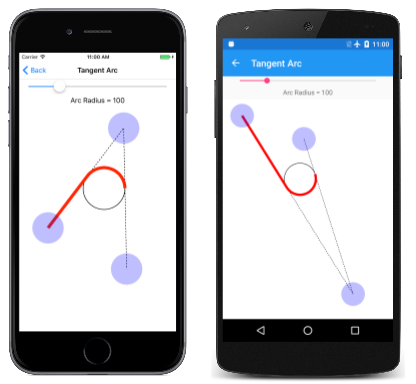
The Tangent Arc page allows you to experiment with the tangent arc. This is the first of several pages that derive from InteractivePage, which defines a few handy SKPaint objects and performs TouchPoint processing:

              public course InteractivePage : ContentPage {     protected SKCanvasView baseCanvasView;     protected TouchPoint[] touchPoints;      protected SKPaint strokePaint = new SKPaint     {         Fashion = SKPaintStyle.Stroke,         Colour = SKColors.Black,         StrokeWidth = three     };      protected SKPaint redStrokePaint = new SKPaint     {         Mode = SKPaintStyle.Stroke,         Colour = SKColors.Red,         StrokeWidth = 15     };      protected SKPaint dottedStrokePaint = new SKPaint     {         Style = SKPaintStyle.Stroke,         Color = SKColors.Black,         StrokeWidth = iii,         PathEffect = SKPathEffect.CreateDash(new bladder[] { 7, 7 }, 0)     };      protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)     {         bool touchPointMoved = false;          foreach (TouchPoint touchPoint in touchPoints)         {             float scale = baseCanvasView.CanvasSize.Width / (bladder)baseCanvasView.Width;             SKPoint point = new SKPoint(scale * (float)args.Location.10,                                         scale * (bladder)args.Location.Y);             touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, betoken);         }          if (touchPointMoved)         {             baseCanvasView.InvalidateSurface();         }     } }                          

The TangentArcPage course derives from InteractivePage. The constructor in the TangentArcPage.xaml.cs file is responsible for instantiating and initializing the touchPoints assortment, and setting baseCanvasView (in InteractivePage) to the SKCanvasView object instantiated in the TangentArcPage.xaml file:

              public partial class TangentArcPage : InteractivePage {     public TangentArcPage()     {         touchPoints = new TouchPoint[3];          for (int i = 0; i < 3; i++)         {             TouchPoint touchPoint = new TouchPoint             {                 Centre = new SKPoint(i == 0 ? 100 : 500,                                      i != ii ? 100 : 500)             };             touchPoints[i] = touchPoint;         }          InitializeComponent();          baseCanvasView = canvasView;         radiusSlider.Value = 100;     }      void sliderValueChanged(object sender, ValueChangedEventArgs args)     {         if (canvasView != zippo)         {             canvasView.InvalidateSurface();         }     }     ... }                          

The PaintSurface handler uses the ArcTo method to draw the arc based on the affect points and a Slider, but also algorithmically calculates the circle that the angle is based on:

              public partial course TangentArcPage : InteractivePage {     ...     void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)     {         SKImageInfo info = args.Info;         SKSurface surface = args.Surface;         SKCanvas canvas = surface.Canvas;          canvas.Clear();          // Depict the two lines that run into at an angle         using (SKPath path = new SKPath())         {             path.MoveTo(touchPoints[0].Center);             path.LineTo(touchPoints[1].Center);             path.LineTo(touchPoints[2].Center);             canvas.DrawPath(path, dottedStrokePaint);         }          // Describe the circle that the arc wraps effectually         float radius = (float)radiusSlider.Value;          SKPoint v1 = Normalize(touchPoints[0].Center - touchPoints[ane].Center);         SKPoint v2 = Normalize(touchPoints[2].Middle - touchPoints[1].Middle);          double dotProduct = v1.X * v2.X + v1.Y * v2.Y;         double angleBetween = Math.Acos(dotProduct);         float hypotenuse = radius / (float)Math.Sin(angleBetween / two);         SKPoint vMid = Normalize(new SKPoint((v1.X + v2.X) / 2, (v1.Y + v2.Y) / ii));         SKPoint centre = new SKPoint(touchPoints[1].Center.X + vMid.10 * hypotenuse,                                      touchPoints[i].Heart.Y + vMid.Y * hypotenuse);          sheet.DrawCircle(center.X, center.Y, radius, this.strokePaint);          // Depict the tangent arc         using (SKPath path = new SKPath())         {             path.MoveTo(touchPoints[0].Center);             path.ArcTo(touchPoints[ane].Center, touchPoints[ii].Centre, radius);             canvas.DrawPath(path, redStrokePaint);         }          foreach (TouchPoint touchPoint in touchPoints)         {             touchPoint.Paint(canvas);         }     }      // Vector methods     SKPoint Normalize(SKPoint v)     {         float magnitude = Magnitude(v);         render new SKPoint(v.X / magnitude, v.Y / magnitude);     }      float Magnitude(SKPoint 5)     {         render (float)Math.Sqrt(v.X * 5.Ten + v.Y * v.Y);     } }                          

Here's the Tangent Arc page running:

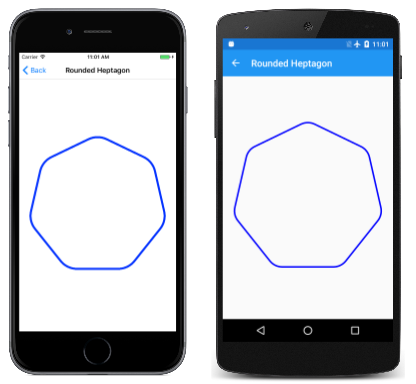
The tangent arc is ideal for creating rounded corners, such every bit a rounded rectangle. Because SKPath already includes an AddRoundedRect method, the Rounded Heptagon page demonstrates how to use ArcTo for rounding the corners of a seven-sided polygon. (The code is generalized for any regular polygon.)

The PaintSurface handler of the RoundedHeptagonPage grade contains ane for loop to calculate the coordinates of the seven vertices of the heptagon, and a second to calculate the midpoints of the seven sides from these vertices. These midpoints are then used to construct the path:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas canvas = surface.Canvas;      canvas.Articulate();      float cornerRadius = 100;     int numVertices = vii;     float radius = 0.45f * Math.Min(info.Width, info.Top);      SKPoint[] vertices = new SKPoint[numVertices];     SKPoint[] midPoints = new SKPoint[numVertices];      double vertexAngle = -0.5f * Math.PI;       // straight upwards      // Coordinates of the vertices of the polygon     for (int vertex = 0; vertex < numVertices; vertex++)     {         vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),                                        radius * (float)Math.Sin(vertexAngle));         vertexAngle += ii * Math.PI / numVertices;     }      // Coordinates of the midpoints of the sides connecting the vertices     for (int vertex = 0; vertex < numVertices; vertex++)     {         int prevVertex = (vertex + numVertices - one) % numVertices;         midPoints[vertex] = new SKPoint((vertices[prevVertex].10 + vertices[vertex].X) / ii,                                         (vertices[prevVertex].Y + vertices[vertex].Y) / 2);     }      // Create the path     using (SKPath path = new SKPath())     {         // Brainstorm at the first midpoint         path.MoveTo(midPoints[0]);          for (int vertex = 0; vertex < numVertices; vertex++)         {             SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];              // Draws a line from the current signal, and and so the arc             path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);              // Connect the arc with the next midpoint             path.LineTo(nextMidPoint);         }         path.Close();          // Render the path in the center of the screen         using (SKPaint paint = new SKPaint())         {             paint.Style = SKPaintStyle.Stroke;             paint.Color = SKColors.Blue;             paint.StrokeWidth = ten;              canvas.Translate(info.Width / 2, info.Height / 2);             sheet.DrawPath(path, paint);         }     } }                          

Here'due south the programme running:

The Elliptical Arc

The elliptical arc is added to a path with a call to the ArcTo method that has two SKPoint parameters, or the ArcTo overload with split up 10 and Y coordinates:

              public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)  public void ArcTo (Single rx, Single ry, Unmarried xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Unmarried y)                          

The elliptical arc is consistent with the elliptical arc included in Scalable Vector Graphics (SVG) and the Universal Windows Platform ArcSegment class.

These ArcTo methods draw an arc between two points, which are the electric current bespeak of the contour, and the final parameter to the ArcTo method (the xy parameter or the divide x and y parameters):

The first bespeak parameter to the ArcTo method (r, or rx and ry) is not a bespeak at all but instead specifies the horizontal and vertical radii of an ellipse;

The xAxisRotate parameter is the number of clockwise degrees to rotate this ellipse:

If this tilted ellipse is and then positioned so that it touches the ii points, the points are continued by ii different arcs:

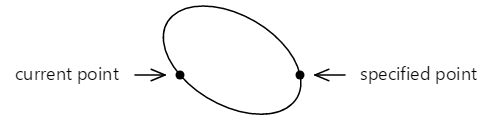
These two arcs tin be distinguished in 2 ways: The meridian arc is larger than the bottom arc, and as the arc is drawn from left to right, the top arc is drawn in a clockwise direction while the bottom arc is drawn in a counter-clockwise management.

It is too possible to fit the ellipse between the two points in another mode:

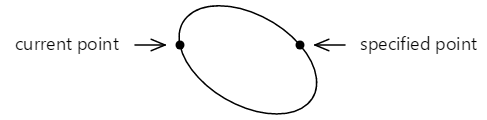
At present there's a smaller arc on top that's drawn clockwise, and a larger arc on the bottom that's drawn counter-clockwise.

These 2 points tin can therefore be connected by an arc defined by the tilted ellipse in a total of 4 ways:

These four arcs are distinguished past the 4 combinations of the SKPathArcSize and SKPathDirection enumeration type arguments to the ArcTo method:

• red: SKPathArcSize.Large and SKPathDirection.Clockwise
• greenish: SKPathArcSize.Small and SKPathDirection.Clockwise
• blue: SKPathArcSize.Small and SKPathDirection.CounterClockwise
• magenta: SKPathArcSize.Large and SKPathDirection.CounterClockwise

If the tilted ellipse is not large enough to fit between the two points, and then it is uniformly scaled until it is large plenty. But two unique arcs connect the two points in that case. These can be distinguished with the SKPathDirection parameter.

Although this arroyo to defining an arc sounds complex on offset encounter, it is the but arroyo that allows defining an arc with a rotated ellipse, and it is frequently the easiest approach when you need to integrate arcs with other parts of the contour.

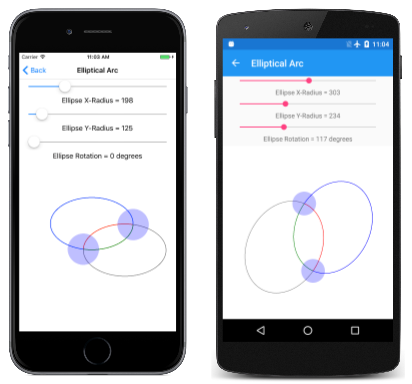
The Elliptical Arc page allows you to interactively set up the two points, and the size and rotation of the ellipse. The EllipticalArcPage form derives from InteractivePage, and the PaintSurface handler in the EllipticalArcPage.xaml.cs lawmaking-behind file draws the four arcs:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas canvas = surface.Canvass;      canvass.Articulate();      using (SKPath path = new SKPath())     {         int colorIndex = 0;         SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,                                           (float)yRadiusSlider.Value);         bladder rotation = (float)rotationSlider.Value;          foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))             foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))             {                 path.MoveTo(touchPoints[0].Center);                 path.ArcTo(ellipseSize, rotation,                            arcSize, management,                            touchPoints[1].Center);                  strokePaint.Color = colors[colorIndex++];                 canvas.DrawPath(path, strokePaint);                 path.Reset();             }     }      foreach (TouchPoint touchPoint in touchPoints)     {         touchPoint.Pigment(canvas);     } }                          

Here it is running:

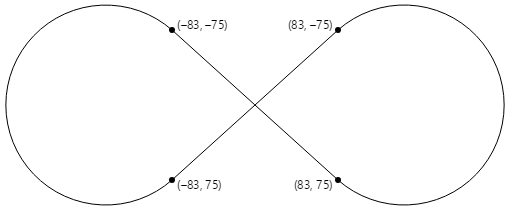
The Arc Infinity page uses the elliptical arc to draw an infinity sign. The infinity sign is based on ii circles with radii of 100 units separated by 100 units:

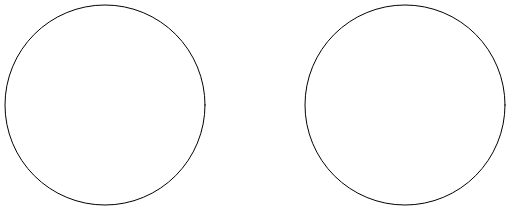
Ii lines crossing each other are tangent to both circles:

The infinity sign is a combination of parts of these circles and the two lines. To utilise the elliptical arc to draw the infinity sign, the coordinates where the two lines are tangent to the circles must be determined.

Construct a right rectangle in ane of the circles:

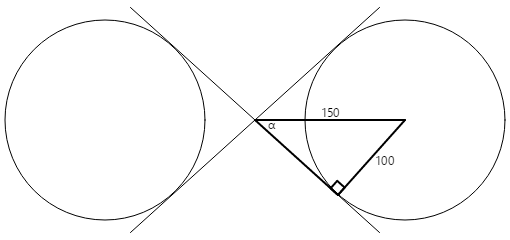
The radius of the circle is 100 units, and the hypotenuse of the triangle is 150 units, so the angle α is the arcsine (inverse sine) of 100 divided past 150, or 41.8 degrees. The length of the other side of the triangle is 150 times the cosine of 41.viii degrees, or 112, which can also be calculated by the Pythagorean theorem.

The coordinates of the tangent point tin can then be calculated using this information:

ten = 112·cos(41.8) = 83

y = 112·sin(41.8) = 75

The iv tangent points are all that's necessary to depict an infinity sign centered on the betoken (0, 0) with circle radii of 100:

The PaintSurface handler in the ArcInfinityPage form positions the infinity sign so that the (0, 0) indicate is positioned in the center of the page, and scales the path to the screen size:

              void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args) {     SKImageInfo info = args.Info;     SKSurface surface = args.Surface;     SKCanvas canvas = surface.Canvas;      sheet.Articulate();      using (SKPath path = new SKPath())     {         path.LineTo(83, 75);         path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);         path.LineTo(-83, 75);         path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);         path.Close();          // Employ path.TightBounds for coordinates without control points         SKRect pathBounds = path.Bounds;          sheet.Translate(info.Width / 2, info.Height / two);         canvas.Scale(Math.Min(info.Width / pathBounds.Width,                               info.Tiptop / pathBounds.Height));          using (SKPaint pigment = new SKPaint())         {             paint.Mode = SKPaintStyle.Stroke;             paint.Colour = SKColors.Bluish;             paint.StrokeWidth = five;              canvas.DrawPath(path, paint);         }     } }                          

The code uses the Premises holding of SKPath to determine the dimensions of the infinity sine to scale it to the size of the sheet:

The result seems a little small, which suggests that the Bounds property of SKPath is reporting a size larger than the path.

Internally, Skia approximates the arc using multiple quadratic Bézier curves. These curves (equally you'll come across in the next section) comprise control points that govern how the curve is drawn but are not part of the rendered curve. The Bounds property includes those control points.

To get a tighter fit, employ the TightBounds belongings, which excludes the control points. Here'south the program running in landscape fashion, and using the TightBounds property to obtain the path bounds:

Although the connections betwixt the arcs and straight lines are mathematically smooth, the change from arc to directly line might seem a little abrupt. A better infinity sign is presented in the next article on Three Types of Bézier Curves.

• SkiaSharp APIs
• SkiaSharpFormsDemos (sample)

Feedback

Submit and view feedback for

payneawareed.blogspot.com

Source: https://docs.microsoft.com/en-us/xamarin/xamarin-forms/user-interface/graphics/skiasharp/curves/arcs

Share this post